3-1 บทนํา

        พีชคณิตบูลีนค้นพบโดย George Boole นัก คณิตศาสตร์ชาวอังกฤษ ประกอบด้วยสมการที่แสดง ความสัมพันธ์ของค่าคงที่และตัวแปร แต่ค่าคงที่ของพีชคณิต บูลีน คือค่าในเลขฐาน 2 (1 และ 0 เท่านั้น) ส่วนค่าคงที่ใน พีชคณิตทั่วไปคือค่าตัวเลขฐาน 10 (ประกอบไปด้วยเลข 0-9) ดังนั้นกฎและสูตรต่าง ๆ ของพีชคณิตบูลีนจึงแตกต่างกว่า ตัว กระทําในพีชคณิตบูลีนมี 3 ตัว คือ แอนด์ (AND ( )) ออร์ (OR (+)) นอต (NOT (-)) และตัวกระทําดังกล่าวเป็ นกฎที่เป็ นจริงเสมอ และตัวกระทํา เหล่านี้ได้มีผู้ศึกษาแล้วว่ามีความสัมพันธ์กันกับลักษณะของวงจรรีเลย์คือ การเปิดและ ปิดหน้าสัมผัสของวงจรรีเลย์เปรียบได้กับตัวแปรในสมการบูลีนกระทําการ AND, OR หรือ NOT กัน ต่อมาเมื่อวิวัฒนาการทางด้านการสร้างวงจรรวมเกี่ยวกับวงจร สวิตชิ่ง มีการพัฒนามากขึ้น จึงมีการสร้างวงจรสวิตชิ่งที่ทําหน้าที่เป็ นตัวกระทํา AND, OR และ NOT บรรจุอยู่ในวงจรรวมแบบตัวถังพลาสติกทั้งชนิดทีทีแอลและซีมอสโดยให้ ชื่อวงจรที่ทําหน้าที่เป็ นตัวกระทําดังกล่าวว่าแอนด์เกตออร์เกต และนอตเกต มี ความสัมพันธ์เหมือนกับวงจรรีเลย์ที่มีการเปิดและปิดของหน้าสัมผัสที่มีความสัมพันธ์กับ พีชคณิตบูลีน จึงนิยมใช้พีชคณิตบูลีนแก้ไขปัญหาทางวงจรดิจิตอลอิเล็กทรอนิกส์เช่นในด้านการออกแบบวงจรดิจิตอลตามเงื่อนไขหรือฟังก์ชันที่กําหนดโดยลักษณะของงานที่ แตกต่างกัน การเปลี่ยนรูปแบบของวงจร และการลดต้นทุนการผลิตวงจร

3-2 กฎของพ ี ชคณิตบ ู ล ี น (Boolean algebra Law’s)

      กฎและสูตรต่าง ๆ ที่เขียนขึ้นมาจากการกระทําตามตัวกระทําของตัวแปรใด ๆ หรือค่าคงที่ใด ๆ กับตัวแปร ซึ่งแยกเป็ น 6 กลุ่ม รวม 21 สูตร คือ

3-3 การลดร ู ปสมการพี ชคณิต บ ู ล ี น (Boolean Expression Reduction)

       การลดรูปสมการพีชคณิตบูลีน (หรือสมการ ลอจิก) ที่มีความยาวมากๆ ให้สั้นลงได้ทําให้เกิดผลดี อย่างมากกับการออกแบบวงจรลอจิก เพราะสมการ บูลีนนั้นมีความสัมพันธ์กับการกระทําของเกตต่าง ๆ และสามารถเขียนวงจรลอจิกแทน ตัวกระทําต่าง ๆ ในสมการบูลีนได้ดังนั้นแทนที่เราจะต้องเสียต้นทุนและเวลาในการ ออกแบบวงจรลอจิกให้มีขนาดเล ็ กลง เราก ็ กลับมาใช้พีชคณิตบูลีนลดรูปสมการของ วงจรลอจิกนั้นเสียก่อนแล้วจึงมาประกอบเป็ นวงจรลอจิกที่เล ็กลงได้อีกครั้งหนึ่ง

3-4 ทฤษฎ ี ด ี มอรแกน ์ (De’morgan Theorem)

            ค้นพบโดยนักคณิตศาสตร์ชาวอังกฤษชื่อ Augustus De Morgan (1806-1871) เป็ นทฤษฎีที่ใช้ประโยชน์ในการ แก้ปัญหาของพีชคณิตบูลีน กรณีที่สมการของตัวแปรใด ๆ ติด เครื่องหมาย ΑΝD และ OR ซึ่งสามารถเปลี่ยนกลับจาก เครื่องหมาย ΑΝD เป็ น OR และเปลี่ยนสมการจากเครื่องหมาย OR เป็ น ΑΝD ได้ขอให้พิจารณา 2 สมการต่อไปนี้

1. Complement function (โดยการใส่เครื่องหมาย ΝΟΤ ตลอดทั้งฟังก์ชัน)  

2. Change operator (เปลี่ยนตัวกระทํา ΑΝD เป็ น OR และ OR เป็ น ΑΝD  

3. Complement variable (ใส่เครื่องหมาย ΝΟΤที่ตัวแปร) 

จากตัวอย่างจะเห ็ นว่าถ้าสมการนั้นมีหลายเทอม ถ้าใช้ดีมอร์แกน ก ็ ต้องทํากับ เครื่องหมาย OR และ ΑΝD ทุกเครื่องหมาย โดยกําหนดให้แต่ละเทอมที่กระทําการ OR หรือ ΑΝD นั้นมีความหมายเหมือนตัวแปรตัวเดียว

หมายเหตุ ตัวอย่าง 3.11 และ 3.12 ให้ผลลัพธ์ที่เท่ากันตัวอย่าง 3.11 ใช้เทคนิคการ สมมติฟังก์ชันเพื่อให้สมการมีรูปแบบที่ดูง่ายกว่าเดิม ตัวอย่าง 3.12 เป็นแนวทางในการ แก้ไขปัญหาการลดรูปสมการพีชคณิตบูลีนที่ดี

3.5 สมการ SOP และสมการ POS (SOP and POS Equation)

 ตารางความจริง (Truth table) คือตารางแสดงการกระทําของตัวกระทํากับตัว แปรใด ๆ ของสมการบูลีน เช่น สมการ Υ = Α + ΒC ก ็ หมายถึง Υ = f ( Α ,Β ,C) ซึ่งตัว แปร Α ,Β ,C กระทําการ ΑΝD,ΟR,ΝΟΤ กัน เป็ นต้น ซึ่งเราสามารถจะแทนค่าคงที่ (0 หรือ 1) แทนในตัวแปร Α ,Β หรือ C เราสามารถบอกได้ว่า Υ หรือ f ( Α ,Β ,C) นั้นมี ค่าเท่าไรและการแทนค่าคงที่ดังกล่าวลงในตัวแปร Α ,Β ,C นั้นก ็ กระทํากันได้ 8 ครั้ง เท่ากับจํานวนบรรทัดของตารางความจริง เนื่องจากจํานวนบรรทัดของตารางความจริง คือ 2 ตัวแปร เช่น ถ้าวงจรลอจิกมีตัวแปรเพียง 2 ตัวแปร จํานวนบรรทัดของตาราง ความจริงคือ 2 2 = 4 บรรทัด หรือกรณีวงจรลอจิกมีตัวแปร 3 ตัวแปรจะมีจํานวน บรรทัดของตารางความจริงเท่ากับ 3 2 บรรทัด (8 บรรทัด) เป็ นต้น

         จากตารางความจริงแสดงค่า f ( Α ,Β ,C) = Α + ΒC จะเห ็ นว่าค่าของ Υ หรือ f ( Α , Β ,C) นั้นจะมีค่าเป็ น 0 หรือ 1 ตามแต่การกระทําของตัวแปรในสมการ Υ = Α + ΒC และค่าของ Υ นี้ก ็ คือเอาต์พุตของสมการ Α + ΒC นั้นเอง อาจเขียนตาราง ความจริงใหม่ให้มีรูปแบบที่ชัดเจนขึ้นดังนี้

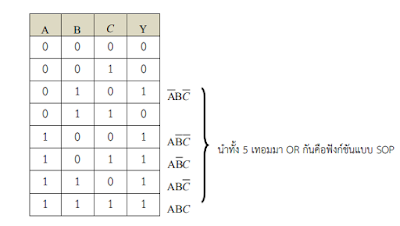
จากตารางความจริงสามารถถอดความสัมพันธ์ในตารางออกมาเป็ นสมการ พีชคณิตบูลีนได้เช่นเดียวกัน วิธีแรกคือ ให้พิจารณาเอาต์พุตที่เป็ น 1 ของตารางความ จริง และเขียนเทอมของตัวแปร Α ,Β ,C ออกมาทีละเทอม โดยแทนค่าตัวแปรที่เป็ น 0 หรือ Α,Β หรือ C และตัวแปรที่เป็ น 1 ด้วย Α ,Β หรือ C ตัวแปรแต่ละตัวกระทําการ ΑΝD กัน และนําเทอมของตัวแปรแต่ละเทอมที่เขียนได้จากเอาต์พุตที่เป็ น 1 มากระทํา ΟR กัน เรียกว่า วิธีเขียนสมการแบบ Sum of Product (SOP) หรือ Min term

สมการพีชคณิตบูลีนแบบ Product of Sum (POS) หรือสมการแบบ Max term รูปแบบของสมการแบบ POS จะตรงข้ามกับสมการแบบ SOP ตั้งแต่การพิจารณา เอาต์พุต การเขียนตัวแปรแต่ละตัว และการติดเครื่องหมาย ΝΟΤ ที่ตัวแปรเหล่านั้น สรุปวิธีการเขียนสมการ POS คือต้องนําเทอมของเอาต์พุตที่มีผลลัพธ์เป็ น 0 มาเขียนโดย กําหนดตัวแปรที่มีค่าเป็ น 0 แทนด้วย Α ,Β หรือ C และตัวแปรที่มีค่าเป็ น 1 แทนด้วย Α,Β หรือ C กระทําการ ΟR กันแล้วนําผลลัพธ์ของการ ΟR ทุก ๆ เทอมที่เป็ น 0 นํามา ΑΝD กัน ก ็จะได้สมการ SOP 

พิจารณาตารางความจริงต่อไปนี

       จากผลการลดรูปสมการ POS จะเห ็ นว่าให้ผลลัพธ์เท่ากันกับการถอดสมการ แบบ SOP จากตารางความจริง ดังนั้นเราจะใช้วิธีถอดสมการแบบใดก็ได้ขึ้นอยู่กับความ เหมาะสมของเอาต์พุตตารางความจริง เช่น ถ้าเอาต์พุตมี “0” มากกว่า “1” เราก ็ควรใช้ วิธี SOP หรือถ้าเอาต์พุตมี “1” มากกว่า “0” ก ็อาจใช้วิธี POS เป็ นต้น เพื่อให้สมการที่ ถอดได้ไม่ยาวมากเกินไป การใช้สมการพีชคณิตบูลีนลดรูปสมการจะผิดพลาดน้อยลง

3.6 การใช้ ตัวเลขแทนสมการ SOP และ POS

 เราสามารถเขียนสมการตัวเลขแทนสมการ SOP ได้โดยกําหนดเครื่องหมาย Σ เข้ากับกลุ่มตัวเลขประจําบรรทัดของตารางความจริงในช่องที่มีเอาต์พุตเป็ น 1 ตัวอย่างเช่น สมการ f( Α , Β,C,D) เท่ากับ ΑΒCD + ΑΒCD + ΑΒCD จะเห ็ นว่าเป็ น สมการ SOP ซึ่งมี 4 ตัวแปร คือ Α ,Β,C, D และเอาต์พุตของสมการนี้จะเป็ น 1 อยู่ 4 บรรทัด คือ (1) บรรทัดที่ ΑΒCD = 0,(2)บรรทัดที่ ΑΒ= 0,CD =1 (3) บรรทัดที่ ΑC = 0,ΒD =1 และ (4) บรรทัดที่ ΑΒD =1และ C = 0 วิธีเขียนตัวเลขแทนสมการให้ทํา ดังนี้

การใช้ตัวเลขแทนสมการ POS ในสมการแบบ SOP นั้น ตัวเลขที่แทนสมการคือ จํานวนบรรทัดแต่ละบรรทัดที่ มีเอาต์พุตเป็ น “1” นํามาร่วมกันภายใต้เครื่องหมาย Σ เช่น f ( Α,Β,C) =Σ (0,2,4,6) เป็ นต้น แต่สมการแบบ POS นั้นจะนับเอาค่าตัวเลขเฉพาะบรรทัดที่มีเอาต์พุตเป็ น “0” มาเขียนรวมกัน ภายใต้เครื่องหมาย π เช่น f ( Α,Β,C)=π (1,3,5,7) เป็ นต้น และต้อง อย่าลืมว่าในสมการแบบ POS นั้น ตัวแปรแต่ละตัวต้องเป็ น NOT เมื่อค่าคงที่ของตัวมัน เป็ น “1” และแต่ละบรรทัดที่เอาต์พุตเป็ น “0” ต้องนําเอาตัวแปรทุกตัวมากระทําการ OR กัน